66 câu trắc nghiệm Phương trình mặt phẳng có đáp án (phần 1)
Câu 1: Trong không gian Oxyz, cho hai điểm A(1;0;-2), B(-1;1;1). Phương trình mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB là:
A. 2x – y – 3z – 8 = 0 C. x – 2z – 8 = 0
B. x – 2z – 8 = 0 D. 2x – y – 3z + 6 = 0
Câu 2: Trong không gian Oxyz, cho hai điểm A(1;3;5), B(-1;5;3). Lập phương trình mặt phẳng trung trực (P) của đoạn thẳng AB
A. x + y + z = 0 B. x + y – z = 0 C. x – y + z = 0 D. -x + y + z = 0
Câu 3: Trong không gian Oxyz, gọi A1, A2, A3 lần lượt là hình chiếu vuông góc của điểm A(4;3;2) trên các trục Ox, Oy, Oz. Trong các khẳng định sau, khẳng định nào sai?
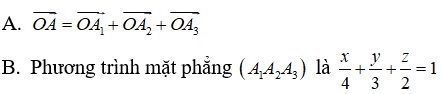
C. Thể tích của tứ diện OA1A2A3 bằng 4
D. Mặt phẳng (A1A2A3) đi qua điểm A.
Câu 4: Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2 ;1 ;-3), vuông góc với mặt phẳng (Q) : x + y – 3z = 0 đồng thời (P) song song với trục Oz.
A. x + y – 3 = 0 B. x – y – 1 = 0 C. 2x + y – 3z – 1 = 0 D. x – y + 1 = 0
Câu 5: Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1 ;0 ;1), B(0 ;-1 ;-3), C(3 ;2 ;5).
A. x – y – 1 = 0 B. x – y + 1 = 0 C. x + z – 2 = 0 D. x + y – 1 = 0
Câu 6: Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1 ;2 ;2) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. 2x + 2y + z – 8 = 0
B. 2x + 2y + z + 8 = 0
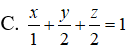
D. x + 2y + 2z – 9 = 0
Câu 7: Trong không gian Oxyz, cho mặt phẳng (P) có phương trình (m2 – 2m)x + y + (m – 1)z + m2 + m = 0, trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) song song với trục Ox ?
A. m=0 B. m=2 C. m=0 hoặc m=2 D. m=1
Câu 8: Trong không gian Oxyz, cho hai mặt phẳng (P) : x + 2y – 2z + 1 = 0, (Q): 2x + 4y + az + b = 0. Tìm a và b sao cho khoảng cách giữa hai mặt phẳng đó bằng 1.
A. a=-4 và b=8 C. a=-2 và b=38 hoặc b=-34
B. a=-4 và b=8 hoặc b=-4 D. a=-4 và b=38 hoặc b=-34
Câu 9: Trong không gian Oxyz, cho mặt cầu (S) có phương trình là x2 + y2 + z2 – 2x – 4y + 6z + 5 = 0 và cho mặt phẳng (P) : x – 2y + 3z + 3 = 0. Khẳng định nào dưới đây là đúng ?
A. (P) giao (S) theo một đường tròn
B. (P) tiếp xúc với (S)
C. (P) không cắt (S)
D. Mặt phẳng (P) đi qua tâm của mặt cầu (S)
Câu 10: Trong không gian Oxyz, cho ba điểm thay đổi A(a; 0; 0), B(0; b; 0), C(0; 0; c) trong đó a, b, c khác 0 và thỏa mãn điều kiện 3ab + bc – 2ac = abc . Khoảng cách lớn nhất từ O đến mặt phẳng (ABC) là:
A. 14 B. √14 C. 1/√14 D. Không tồn tại
Câu 11: Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(x0, y0, z0) và có một vectơ pháp tuyến nP→ = (A; B; C) là:
A. Ax0 + By0 + Cz0 = 0
B. A(x + x0) + B(y + y0) + C(z + z0) = 0
C. A(x – x0) + B(y – y0) + C(z – z0) = 0
D. x0(x – A) + y0(y – B) + z0(z – C) = 0
Câu 12: Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(-x0, y0, -z0) và có một vectơ pháp tuyến nP→ = (-A; B; -C) là:
A. A(x – x0) – B(y – y0) + C(z – z0) = 0
B. A(x + x0) – B(y – y0) + C(z + z0) = 0
C. A(x – x0) – B(y + y0) + C(z – z0) = 0
D. A(x + x0) – B(y + y0) + C(z + z0) = 0
Câu 13: Trong không gian Oxyz, cho điểm M(-x0; -y0; z0) và phương trình của mặt phẳng (P): Ax + By + Cz = D = 0 . Khoảng cách từ điểm M đến mặt phẳng (P) là:
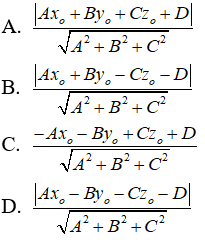
Câu 14: Trong không gian Oxyz, cho hai mặt phẳn song song (P): Ax + By + Cz + D = 0 và (Q): Ax + By + Cz + D’ = 0. M là một điểm di động trên mặt phẳng (P). Khẳng định nào dưới đây có thể sai?
A. Khoảng cách từ điểm M đến mặt phẳng (Q) không phụ thuộc vào M.
B. Khoảng cách giữa hai mặt phẳng (P) và (Q) chính là khoảng cách từ M đến mặt phẳng (Q)
C. Khoảng cách giữa hai mặt phẳng (P) và (Q) là
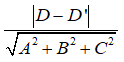
D. Khoảng cách giữa hai mặt phẳng (P) và (Q) là |D’ – D|
Câu 15: Trong các khẳng định dưới đây, khẳng định nào đúng?
A. Mỗi mặt phẳng chỉ có duy nhất một vectơ pháp tuyến
B. Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A thuộc (P) và biết một vectơ pháp tuyến của mặt phẳng (P)
C. Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A thuộc (P) và (P) vuông góc với một mặt phẳng (Q) cho trước
D. Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A thuộc (P) và (P) song song với một đường thẳng d cho trước
Câu 16: Trong các khẳng định dưới đây, khẳng định nào sai?
A. Phương trình của mặt phẳng (P) đi qua điểm M(x0; y0; z0) và có một vectơ pháp tuyến nP→ = (A; B; C) là: A(x – x0) + B(y – y0) + C(z – z0) = 0
B. Nếu hai mặt phẳng vuông góc với nhau thì hai vectơ pháp tuyến của chúng cũng vuông góc
C. Nếu hai mặt phẳng cắt nhau thì hai vectơ pháp tuyến của chúng không cùng phương
D. Nếu hai mặt phẳng (P) và (Q) có hai vectơ pháp tuyến cùng phương thì chúng song song