Hàm số đồng biến nghịch biến khi nào? Lý thuyết & bài tập

Đồng biến, nghịch biến là một trong những tính chất quan trọng và được vận dụng rất nhiều trong khảo sát hàm số. Nhằm giúp bạn đọc nắm vững kiến thức của chuyên đề này, VerbaLearn đã biên soạn bài học khá chi tiết giúp bạn đọc dễ dàng tóm gọn kiến thức và có thêm nhiều ví dụ để vận dụng. Hãy cùng theo dõi dưới đây nhé.

Mục lục1.Hàm số đồng biến, nghịch biến khi nào?2.Phân dạng bài tập tính đồng biến nghịch biến của hàm số

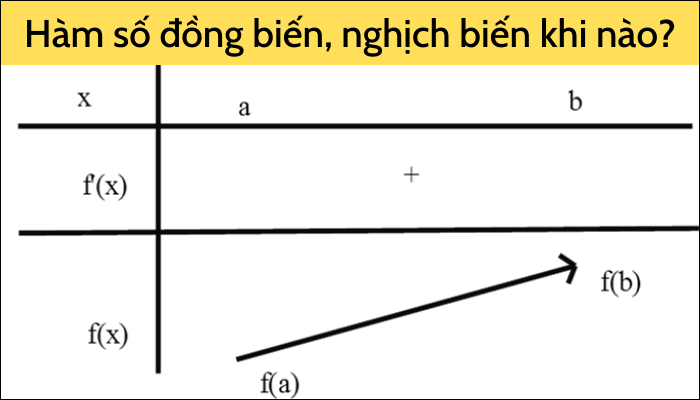
Hàm số đồng biến, nghịch biến khi nào?

Giả sử K là một khoảng, một đoạn hoặc một nữa khoảng và y = f(x) là một hàm số xác định trên K.

+ Hàm số y = f(x) được gọi là đồng biến (tăng) trên K nếu: ∀ x1, x2 ∊ f (x1) < f (x2)

+ Hàm số y = f(x) được gọi là nghịch biến (giảm) trên K nếu: ∀ x1, x2 ∊ f (x1) > f (x2)

Hàm số đồng biến hoặc nghịch biến trên K gọi chung là đơn điệu trên K.

Nhận xét 1

Nếu hàm số f(x) và g(x) cùng đồng biến (nghịch biến) trên D thì hàm số f(x) + g(x) cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng đối với hiệu f(x) – g(x)

Nhận xét 2

Nếu hàm số f(x) và g(x) là các hàm số dương và cùng đồng biến (nghịch biến) trên D thì hàm số f(x)․g(x) cũng đồng biến (nghịch biến) trên D. Tính chất này có thể không đúng khi các hàm số f(x) và g(x) không là các hàm số dương trên D.

Nhận xét 3

Cho hàm số u = u(x) xác định với x ∊ (a;b) và u(x) ∊ (c;d). Hàm số f [u(x)] cũng xác định với x ∊ (a;b). Ta có nhận xét sau:

Giả sử hàm số u = u(x) đồng biến với x ∊ (a;b). Khi đó, hàm số f [u(x)] đồng biến với x ∊ (a;b) ⇔ f(u) đồng biến với u(x) ∊ (c;d)

Giả sử hàm số u = u(x) nghịch biến với x ∊ (a;b). Khi đó, hàm số f [u(x)] nghịch biến với x ∊ (a;b) ⇔ f(u) nghịch biến với u(x) ∊ (c;d)

Định lí 1

Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:

• Nếu hàm số đồng biến trên khoảng K thì f’(x) ≥ 0, ∀ x ∊ K
• Nếu hàm số nghịch biến trên khoảng K thì f’(x) ≤ 0, ∀ x ∊ K

Định lí 2.

Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:

• Nếu f’(x) > 0, ∀ x ∊ K thì hàm số f đồng biến trên K.
• Nếu f’(x) < 0, ∀ x ∊ K thì hàm số f nghịch biến trên K.
• Nếu f’(x) = 0, ∀ x ∊ K thì hàm số f không đổi trên K.

Chú ý: Khoảng K trong định lí trên ta có thể thay thế bởi đoạn hoặc một nửa khoảng. Khi đó phải có thêm giả thuyết “Hàm số liên tục trên đoạn hoặc nửa khoảng đó”. Chẳng hạn:

Nếu hàm số f liên tục trên đoạn [a;b] và f’(x) > 0, ∀ x ∊ (a;b) thì hàm số f đồng biến trên đoạn [a;b]. Ta thường biểu diễn qua bảng biến thiên như sau:

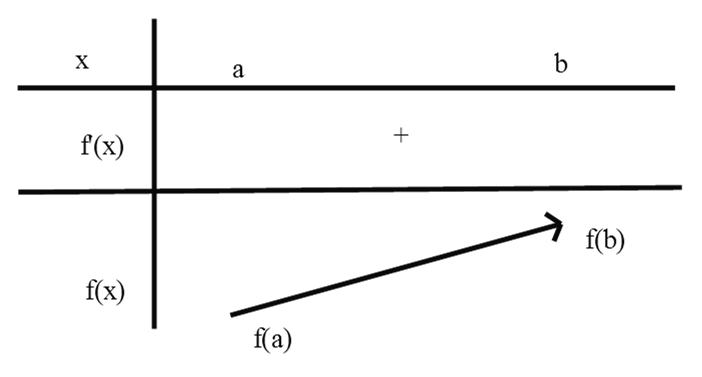
Định lí 3. (mở rộng của định lí 2)

Giả sử hàm số f có đạo hàm trên khoảng K. Khi đó:

• Nếu f’(x) ≥ 0, ∀ x ∊ K và f’(x) = 0 chỉ tại hữu hạn điểm thuộc K thì hàm số f đồng biến trên K.
• Nếu f’(x) ≤ 0, ∀ x ∊ K và f’(x) = 0 chỉ tại hữu hạn điểm thuộc K thì hàm số f nghịch biến trên K.

Phân dạng bài tập tính đồng biến nghịch biến của hàm số

Dạng 1: Tìm khoảng đồng biến – nghịch biến của hàm số

Cho hàm số y = f(x)

+) f’(x) > 0 ở đâu thì hàm số đồng biến ở đấy.

+) f’(x) < 0 ở đâu thì hàm số nghịch biến ở đấy.

Quy tắc:

+) Tính f’(x), giải phương trình f’(x) = 0 tìm nghiệm.

+) Lập bảng xét dấu f’(x)

+) Dựa vào bảng xét dấu và kết luận.

Ví dụ 1. Cho hàm số f(x) đồng biến trên tập số thực ℝ, mệnh đề nào sau đây là đúng?

A. Với mọi x1 > x2 ∊ ℝ ⇒ f (x1) < f (x2)

B. Với mọi x1, x2 ∊ ℝ ⇒ f (x1) > f (x2)

C. Với mọi x1, x2 ∊ ℝ ⇒ f (x1) < f (x2)

D. Với mọi x1 < x2 ∊ ℝ ⇒ f (x1) < f (x2)

Hướng dẫn giải:

Chọn đáp án D.

Ta có: f(x) đồng biến trên tập số thực ℝ.

⇒ x1 < x2 ∊ ℝ ⇒ f (x1) < f (x2)

Ví dụ 2. Cho hàm số f(x) = -2×3 + 3×2 – 3x và 0 ≤ a < b. Khẳng định nào sau đây sai?

A. Hàm số nghịch biến trên ℝ

B. f (a) > f (b)

C. f (b) < 0

D. f (a) < f (b)

Hướng dẫn giải:

Chọn đáp án D.

Ta có: f’(x) = -6×2 + 6x – 3 < 0, ∀ x ∊ ℝ

⇒ Hàm số nghịch biến trên ℝ.

0 ≤ a < b ⇒ f (0) ≥ f (a) > f (b)

Dạng 2: Tìm điều kiện của tham số

Kiến thức chung

+) Để hàm số đồng biến trên khoảng (a;b) thì f’(x) ≥ 0, ∀ x ∊ (a;b).

+) Để hàm số nghịch biến trên khoảng (a;b) thì f’(x) ≤ 0, ∀ x ∊ (a;b).

*) Riêng hàm số: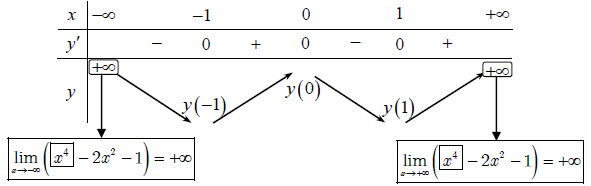

. Có TXĐ là tập D. Điều kiện như sau:

+) Để hàm số đồng biến trên TXĐ thì y’ > 0, ∀ x ∊ D.

+) Để hàm số nghịch biến trên TXĐ thì y’ < 0, ∀ x ∊ D.

+) Để hàm số đồng biến trên khoảng (a;b) thì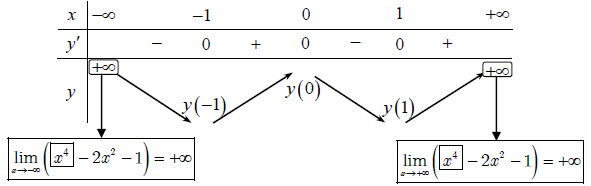

+) Để hàm số nghịch biến trên khoảng (a;b) thì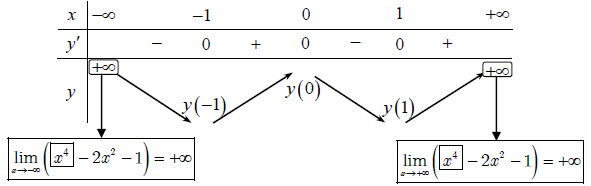

*) Tìm m để hàm số bậc 3 y = ax3 + bx2 + cx + d đơn điệu trên ℝ

+) Tính y = 3ax2 + 2bx + c là tam thức bậc 2 có biệt thức ∆.

+) Để hàm số đồng biến trên ℝ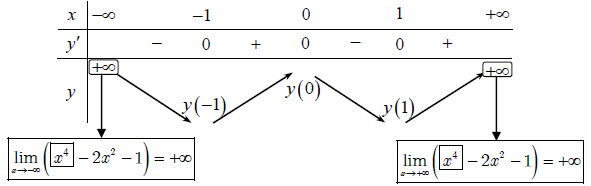

+) Để hàm số nghịch biến trên ℝ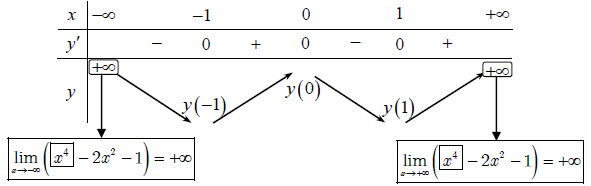

Chú ý: Cho hàm số y = ax3 + bx2 + cx + d

+) Khi a > 0 để hàm số nghịch biến trên một đoạn có độ dài bằng k ⇔ y’ = 0 có 2 nghiệm phân biệt x1, x2 sao cho |x1 – x2| = k

+) Khi a < 0 để hàm số đồng biến trên một đoạn có độ dài bằng k ⇔ y’ = 0 có 2 nghiệm phân biệt x1, x2 sao cho |x1 – x2| = k

Ví dụ 1. Hàm số y = x3 – 3×2 + (m – 2) x + 1 luôn đồng biến khi:

A. m ≥ 5

B. m ≤ 5

C.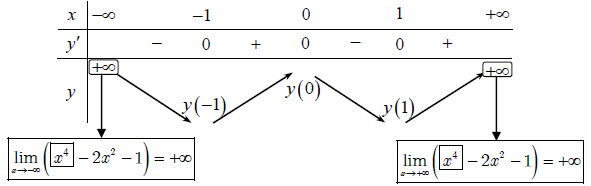

D.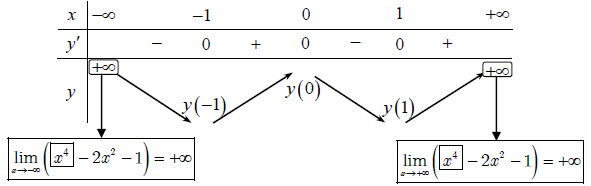

Hướng dẫn giải:

Chọn đáp án A.

Ta có: y’ = 3×2 – 6x + m – 2

Hàm số đồng biến trên ℝ khi và chỉ khi y’ = 3×2 – 6x + m – 2 ≥ 0, ∀ x ∊ ℝ

⇔ ∆’ ≤ 0 ⇔ 15 – 3m ≤ 0 ⇔ m ≥ 5

Ví dụ 2. Hàm số y = ⅓x3 – mx2 – (3m + 2) x + 1 đồng biến trên ℝ khi m bằng

A.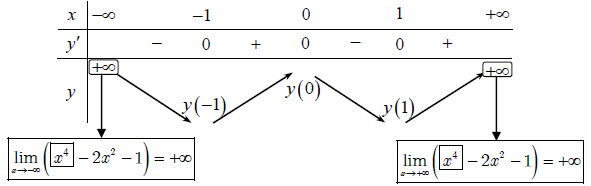

B.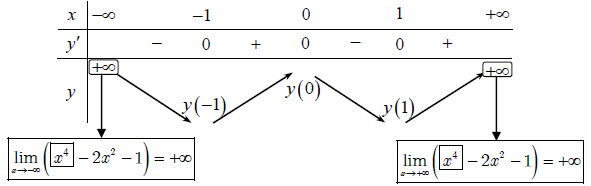

C. -2 ≤ m ≤ -1

D. -2 < m < -1

Hướng dẫn giải:

Chọn đáp án C

Ta có: y’ = x2 – 2mx – 3m + 2

Hàm số đồng biến trên ℝ khi và chỉ khi y’ = x2 – 2mx – 3m + 2 ≥ 0, ∀ x ∊ ℝ

⇔ ∆’ ≤ 0 ⇔ m2 + 3m + 2 ≤ 0 ⇔ -2 ≤ m ≤ -1

Dạng 3: Xét tính đơn điêu hàm số trùng phương

Bước 1: Tìm tập xác định

Bước 2: Tính đạo hàm f’(x) = 0. Tìm các điểm xi (i= 1, 2,… n) mà tại đó đạo hàm bằng 0 hoặc không xác định.

Bước 3: Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.

Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Ví dụ 1. Xét tính đơn điệu của mỗi hàm số sau: y = x4 – 2×2 + 1

Hàm số xác định với mọi x ∊ ℝ

y’ = 4×3 – 4x = 4x (x2 – 1)

Cho y’ = 0 ⇒ x = 0 hoặc x = -1 hoặc x = 1

Bảng biến thiên:

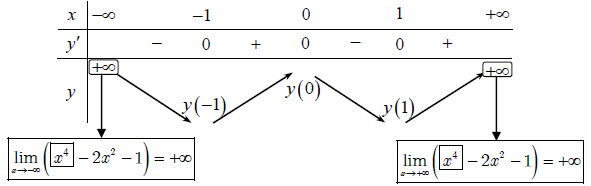
Dựa vào bảng biến thiên suy ra:

• Hàm số đồng biến trên các khoảng (-1;0) và (1; +∞).
• Hàm số nghịch biến trên các khoảng (-∞; -1) và (0;1)

Ví dụ 2. Xét tính đơn điệu của mỗi hàm số sau: y = -x4 + x2 – 2

Hàm số xác định với mọi x ∊ ℝ

y’ = -4×3 + 2x = 2x (-2×2 + 1)

Cho y’ = 0 ⇒ x = 0 hoặc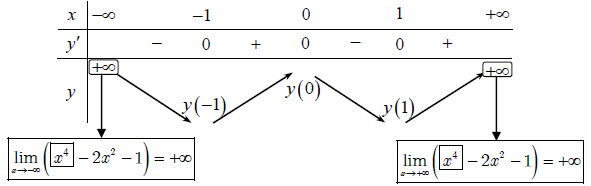

hoặc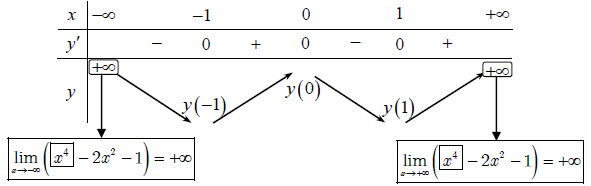

Bảng biến thiên:

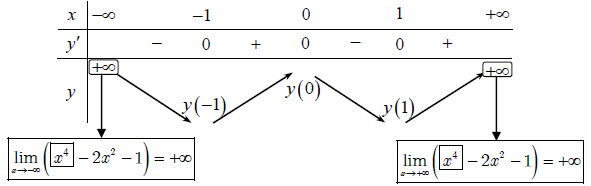
Dựa vào bảng biến thiên suy ra:

Hàm số đồng biến trên các khoảng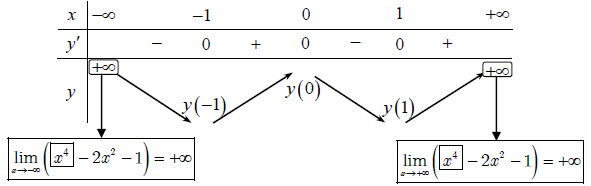

và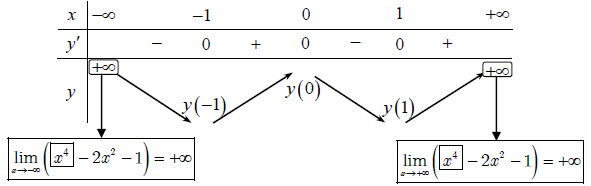

Hàm số nghịch biến trên các khoảng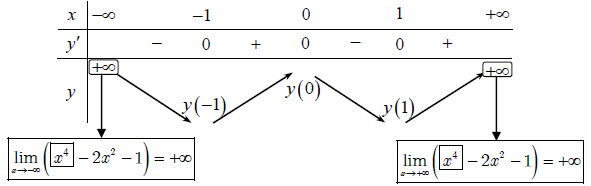

và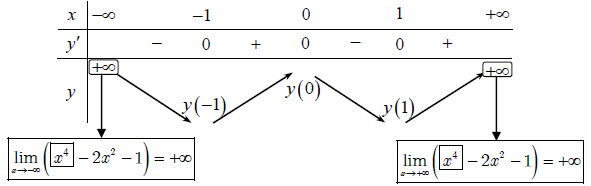

Ví dụ 3. Xét tính đơn điệu của mỗi hàm số sau: y = ¼x4 + 2×2 – 1

Hàm số xác định với mọi x ∊ ℝ

y’ = x3 + 4x = x (x2 + 4)

Cho y’ = 0 ⇒ x = 0 (do x2 + 4 = 0 vô nghiệm)

Bảng biến thiên:

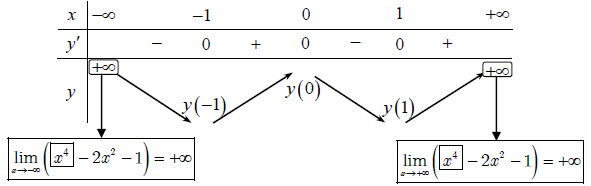
Dựa vào bảng biến thiên suy ra:

• Hàm số đồng biến trên khoảng (0; +∞)
• Hàm số nghịch biến trên khoảng (-∞; 0)

Bài học trên đã trình bày chi tiết về tính đồng biến, nghịch biến của hàm số và hàng loạt các dạng bài liên quan. Đây là một trong những dạng toán nhỏ phổ biến trong các kì thi toán học. Nếu bạn đọc có thắc mắc gì về bài viết có thể để lại bình luận xuống phía bên dưới.