- 1. Cho tam giác ABC cân tại A. Các đường phân giác BD, CE
- 2. Lý thuyết tam giác đồng dạng
- 2.1 Khái niệm hai tam giác đồng dạng
- 2.2 Các trường hợp đồng dạng của tam giác
- 2.3 Các trường hợp đồng dạng của tam giác vuông
- 2.4 Tính chất của tam giác đồng dạng
- 2.5 Định lí hai tam giác đồng dạng
- 3. Định lý Talet
- 3.1 .Tỉ số của hai đoạn thẳng
- 3.2 Đoạn thẳng tỉ lệ
Dạng toán tam giác đồng dạng
Tam giác đồng dạng là một bài học thú vị trong chương trình toán lớp 8. Trong bài viết này, Hoatieu.vn gửi đến bạn đọc dạng toán tam giác đồng dạng.
1. Cho tam giác ABC cân tại A. Các đường phân giác BD, CE
So sánh AE/EB và AD/DC? Tam giác ADE và tam giác ACB có đồng dạng không?
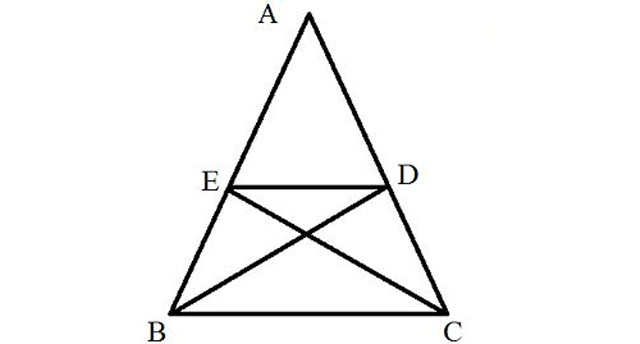
Tam giác ABC cân tại A => ∠ABC = ∠ACB và AB = AC
Xét tam giác BCE và CBD, có:
=> Tam giác BCE = CBD
=> BE = CD => AE = AD
=>
=> ED // BC
Xét tam giác ADE và ACB có:
=> Tam giác ADE ∼ ACB
2. Lý thuyết tam giác đồng dạng
2.1 Khái niệm hai tam giác đồng dạng
Hai tam giác được xem là đồng dạng nếu chúng có 3 cặp góc bằng nhau từng đôi một và 3 cặp cạnh tương ứng tỷ lệ
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu : Các góc: A’ = A ; B’ = B ; C’ = C
Tỉ lệ các cạnh: A’B/AB = B’C’/BC = C’A’/CA
Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
2.2 Các trường hợp đồng dạng của tam giác
Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng với nhau.
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
2.3 Các trường hợp đồng dạng của tam giác vuông
Hai tam giác vuông đồng dạng với nhau nếu :
2.4 Tính chất của tam giác đồng dạng
Hai tam giác A’B’C’ và ABC đồng dạng có một số tính chất:
∆ABC ~ ∆A’B’C’
2.5 Định lí hai tam giác đồng dạng
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
Định lí cũng đúng cho trường hợp đường thẳng a cắt phần kéo dài của hai tam giác song song với cạnh còn lại.
3. Định lý Talet
3.1 .Tỉ số của hai đoạn thẳng
Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
Tỉ số của hai đoạn thẳng được ký hiệu là
3.2 Đoạn thẳng tỉ lệ
Định nghĩa: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức
hoặc
Trên đây, Hoatieu.vn đã gửi đến bạn đọc một số bài toán dạng Tam giác đồng dạng. Mời các bạn đọc thêm các bài viết liên quan tại mảng Tài liệu


























